Introduction

The Monty Hall problem is a famous probability puzzle named after the host of the American television game show "Let's Make a Deal," Monty Hall. The problem is deceptively simple yet has a counterintuitive solution that often confuses people. In this article, we will delve into the Monty Hall problem, explore its mathematical foundations and understand why the optimal strategy may not be immediately obvious.

The Problem

Imagine you are a contestant on a game show. The host presents you with three doors. Behind one of the doors is a brand new car, while the other two doors hide goats. Your goal is to select the door with the car behind it.

You make your initial choice, let's say Door 1. Before revealing what is behind your chosen door, the host, who knows what is behind each door, opens another door that you did not choose, revealing a goat. Now, you are left with two closed doors - your initial choice (Door 1) and the remaining unopened door (Door 2 or Door 3).

At this point, the host gives you a choice: stick with your original selection (Door 1) or switch to the other unopened door. What should you do to maximise your chances of winning the car?

The Counterintuitive Solution

Intuitively, it may seem that switching or sticking with your initial choice should not make a difference. After all, there are only two doors left, so the probability of the car being behind either door should be 50/50, right?

Surprisingly, this intuition is incorrect. The optimal strategy is to always switch. Switching doors gives you a higher probability of winning the car compared to sticking with your initial choice. Let's understand why.

Understanding the Probability

To understand why switching is the better strategy, let's analyse the probabilities involved.

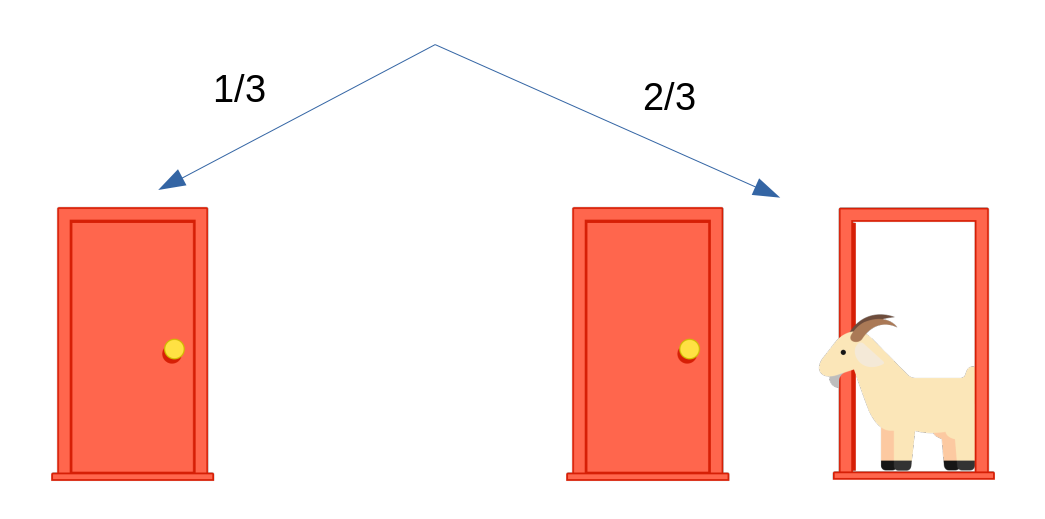
1. Initially, you have a 1/3 chance of choosing the door with the car and a 2/3 chance of selecting a door with a goat.
2. When the host opens a door revealing a goat, the probability distribution changes. The 1/3 chance of selecting a goat door remains with your initial choice, while the remaining unopened door now has a 2/3 chance of hiding the car.

By switching doors, you effectively transfer your initial 1/3 probability to the remaining unopened door, which now has a 2/3 chance of concealing the car. This is why switching gives you a higher probability of winning.

Simulating the Monty Hall Problem

To further illustrate the advantage of switching, let's simulate the Monty Hall problem using a simple program. We will run multiple trials and compare the win rates of the switch and stick strategies.

import random

def simulate_monty_hall(switch_strategy, num_trials):
    wins = 0

    for _ in range(num_trials):
        doors = ['car', 'goat', 'goat']
        random.shuffle(doors)

        chosen_door = random.randint(0, 2)

        # Host opens a goat door
        for i in range(3):
            if i != chosen_door and doors[i] == 'goat':
                doors[i] = 'opened_goat'
                break

        if switch_strategy:
            chosen_door = [i for i in range(3) if i != chosen_door and doors[i] != 'opened_goat'][0]

        if doors[chosen_door] == 'car':
            wins += 1

    return wins / num_trials

num_trials = 1000000
switch_win_rate = simulate_monty_hall(True, num_trials)
stick_win_rate = simulate_monty_hall(False, num_trials)

print(f"Switch strategy win rate: {switch_win_rate * 100:.2f}%")
print(f"Stick strategy win rate: {stick_win_rate * 100:.2f}%")

Running this simulation with a large number of trials (e.g., 1,000,000), we can observe that the win rate for the switch strategy is close to 66.67%, while the win rate for the stick strategy is approximately 33.33%. This supports the mathematical analysis and demonstrates the advantage of switching doors.

Conclusion

The Monty Hall problem is a fascinating probability puzzle that challenges our intuitions. Despite the initial 50/50 appearance, the optimal strategy is to always switch doors. By understanding the underlying probability distribution, we can see why switching gives us a higher chance of winning the car. So, the next time you find yourself on a game show with three doors, remember to switch and increase your odds of driving away in a brand new car!